今天和大家讲一道很火的面试题——64匹马8赛道选前8的算法解析。

题目

有64匹马，一共有8个赛道，想要找出最快的8匹马，要比赛最少多少轮才可以?

解析

这道题初步一看会让人觉得摸不到头脑。

我们试着先用图表示下。

假设每一匹马是一个图的一个节点，用有向线段A->B表示马A比马B快

最终我们可以找到一条从最快马到最慢马的单向路径。

那么我们可以有这样的约束：

• 如果有A->B，A->C，B->C，我们只保留A与C之间最长的路径

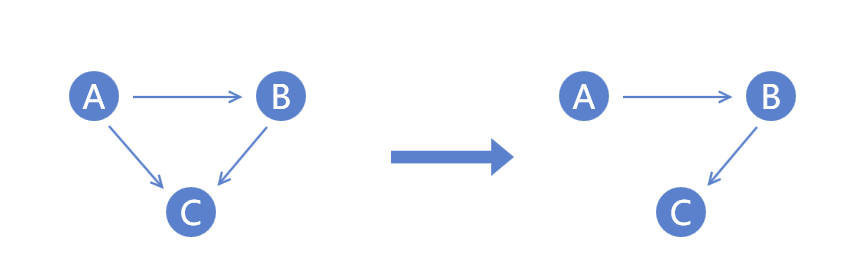
• 如果从起始点出发，任意两点的路径长度一致，意味着这两点之间仍然需要比赛确定名次。

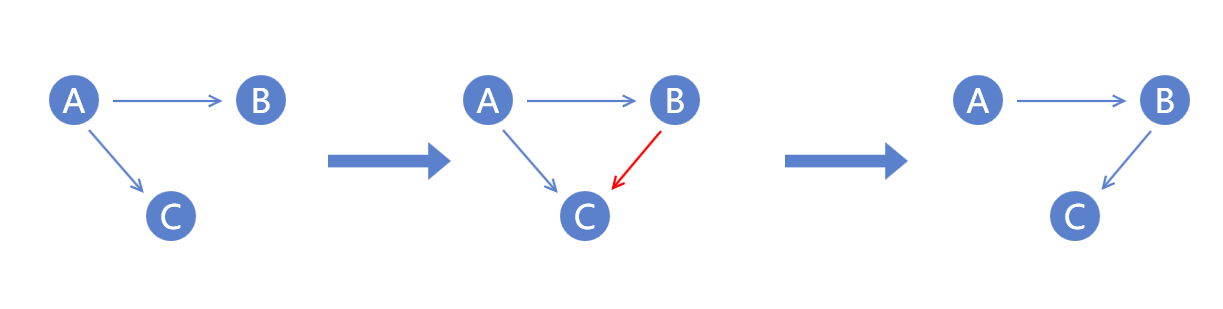
所以我们就可以先搭建这样一个节点图。

这里每一个节点的数字代表马的真实排名，当然我们现在只是作为上帝视角知道这个排名。

我们首先随机分成8组进行比赛，可以获得如下的有向图

为了实现连通，这里增加了一个dumb节点，表示所有节点的起始节点

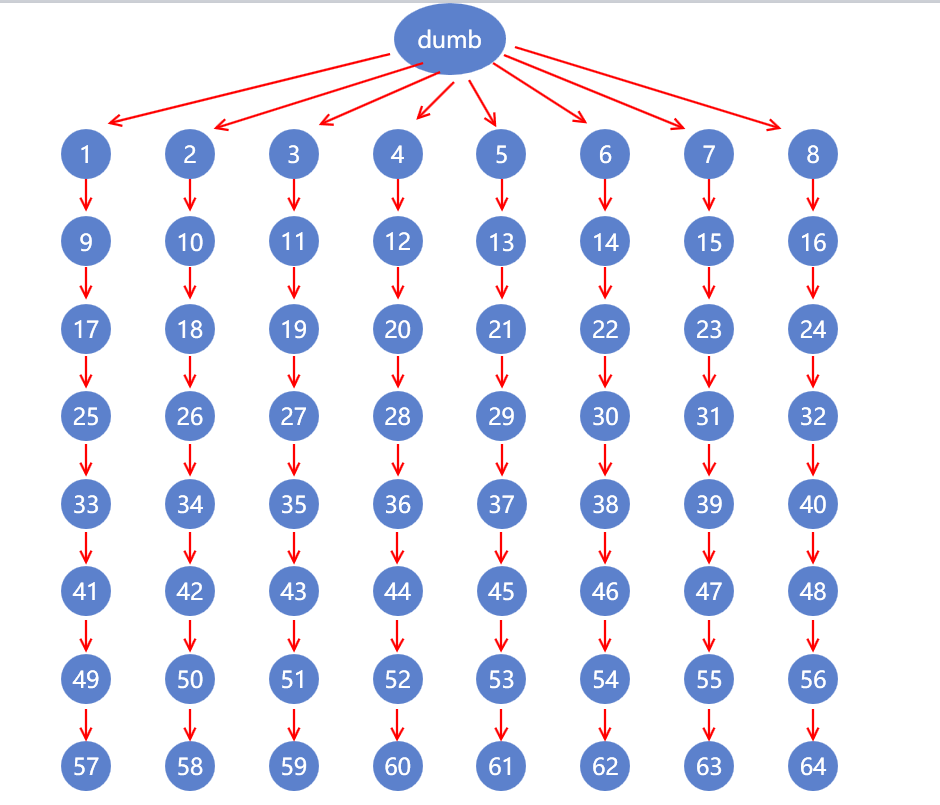
可以看到例如1-8节点同dumb节点的距离都是1，9-16节点同dumb节点的距离都是1，不满足约束。

所以1-8节点之间，9-16节点之间都需要进行比赛。

但是哪一些先比呢？

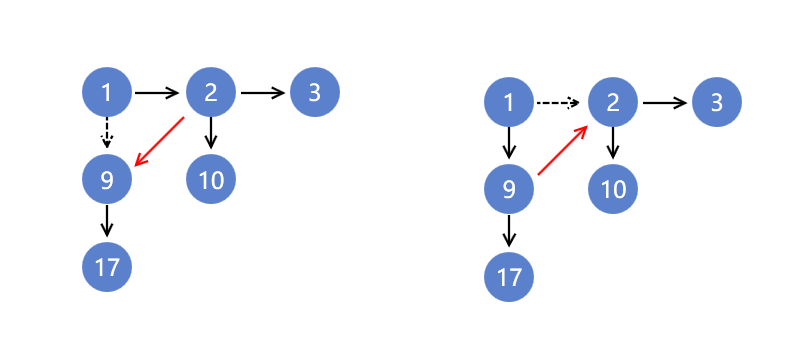
我们可以看到，如果节点1和节点2先比，且节点1比节点2快，那么dumb同节点2所在的子树中所有节点的距离都会加1，所以节点9同节点10 的快慢也自然出现了。

因此我们就可以总结出第三条约束：

• 如果有多组相同距离的节点需要比较，优先让距离短的节点进行比较。

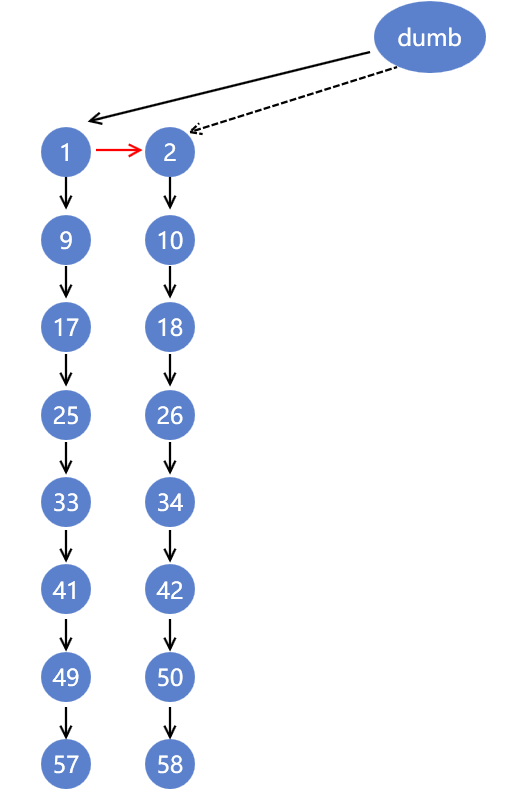
OK，我们对节点1-8进行比赛。

我们可以看到同dumb节点距离为1的节点现在只有一个，即第一名已经获得。

我们还看到图中半透明的节点在这一轮之后距离已经大于8，所以直接可以再算法中抛弃

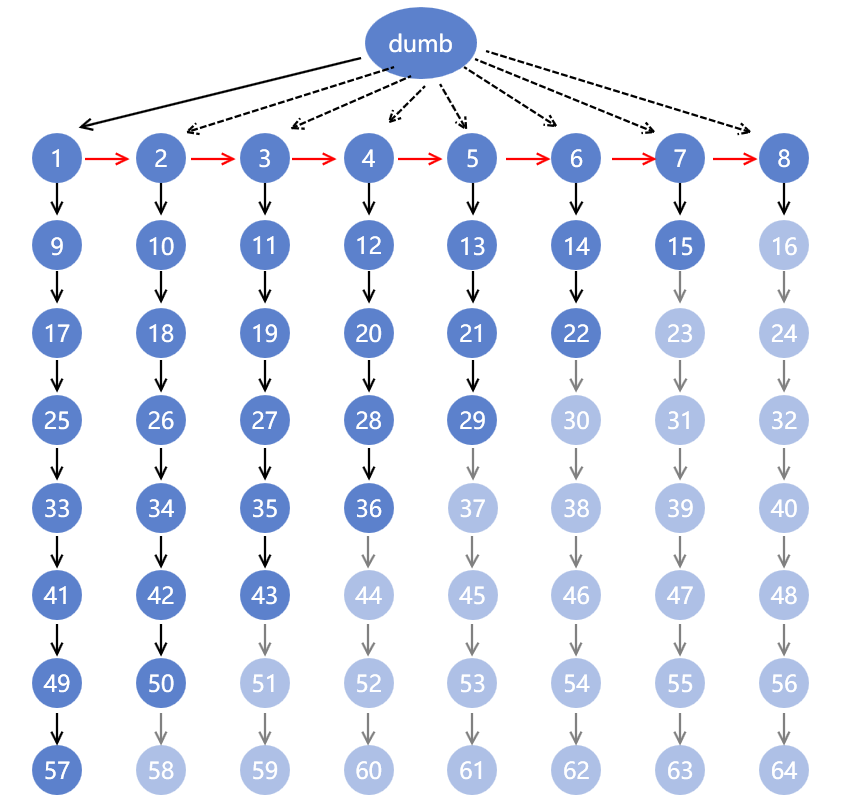
所以简化图形得到如下结果

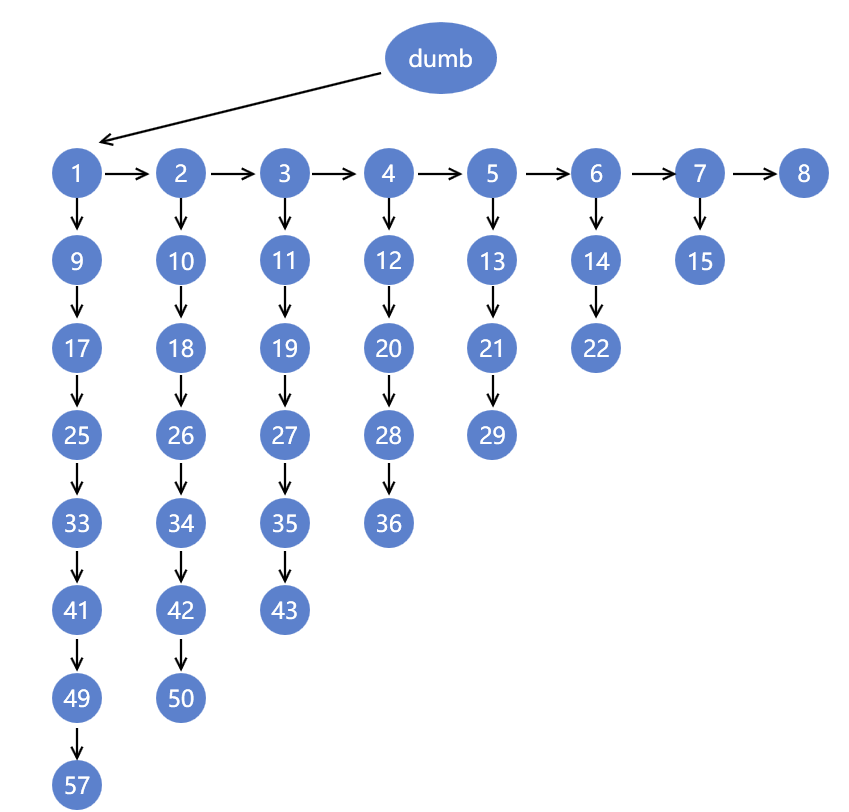
此时同dumb距离为1的节点只有1个，满足约束。

节点2和节点9 同dumb距离都为2 ，需要进行比赛。

但是一次比赛有8个赛道呢，不可能只拿2匹马进行比较。

这里我们分析下，如果节点2赢了，那么节点3,9,10距离都是3，需要进行比较；

如果节点9赢了，节点2，17距离都是3需要进行比较。

所以我们可以把距离为3的节点3,10,17加入进行一起比赛。

此时我们已经有了5匹马，还差3匹。但是距离为4的节点中有4匹马

这里在决策上我们只能任意选择其中的3匹。

因此结果从这里开始变化。

在加入距离为3的节点之前，我们可以出现的关系如图

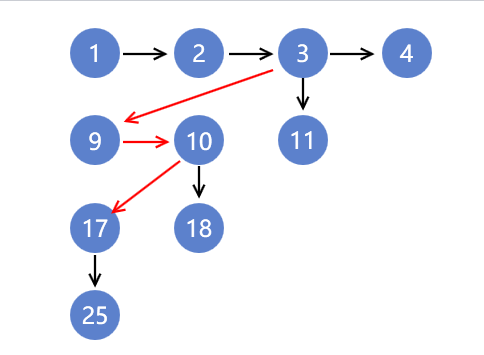
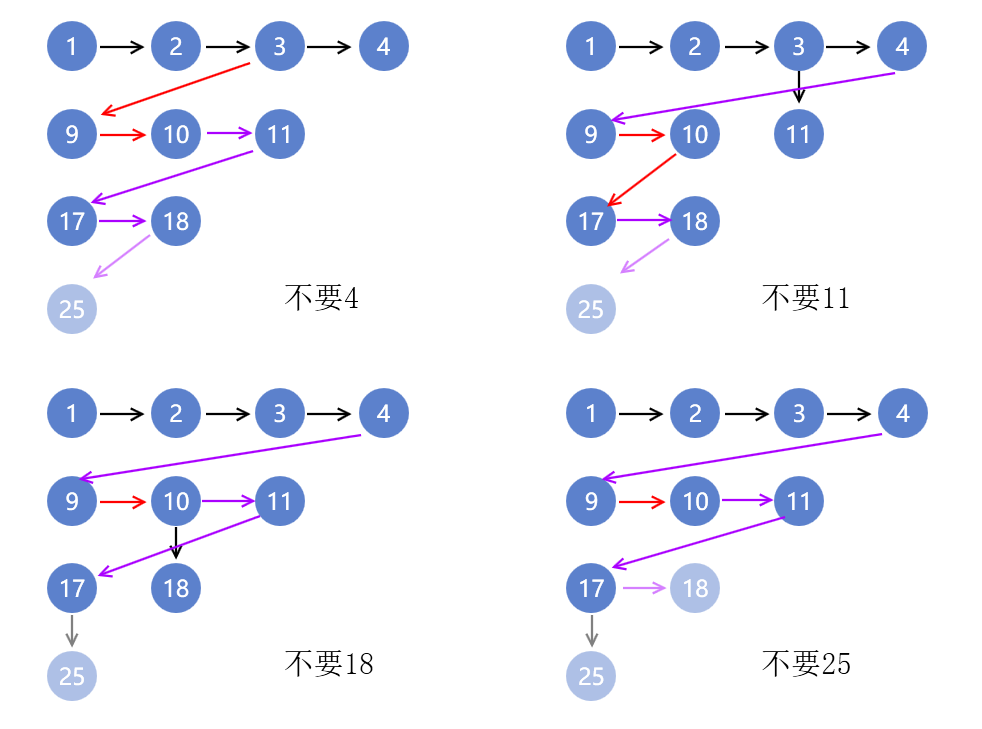
然后我们分别看看4种分支情况结果。

显然节点25在4种情况下都被淘汰，那么它参与比赛的意义都不大，因此不要节点25是最优

而相对的，节点9,10,11,17,18,都有可能是潜在的第4名，所以我们知道节点一定“需要”一次比赛，“战胜”这些潜在对手。因此不要节点4参与比赛的情况是最坏的。

因此我们可以得到另一条“潜在规则”：

• 让事实上更快的节点优先参与比赛，可以得到次数的下限
• 让事实上更快的节点最后参与比赛，可以得到次数的上限

最少次数

所以我们如果选择最少次数结果如下

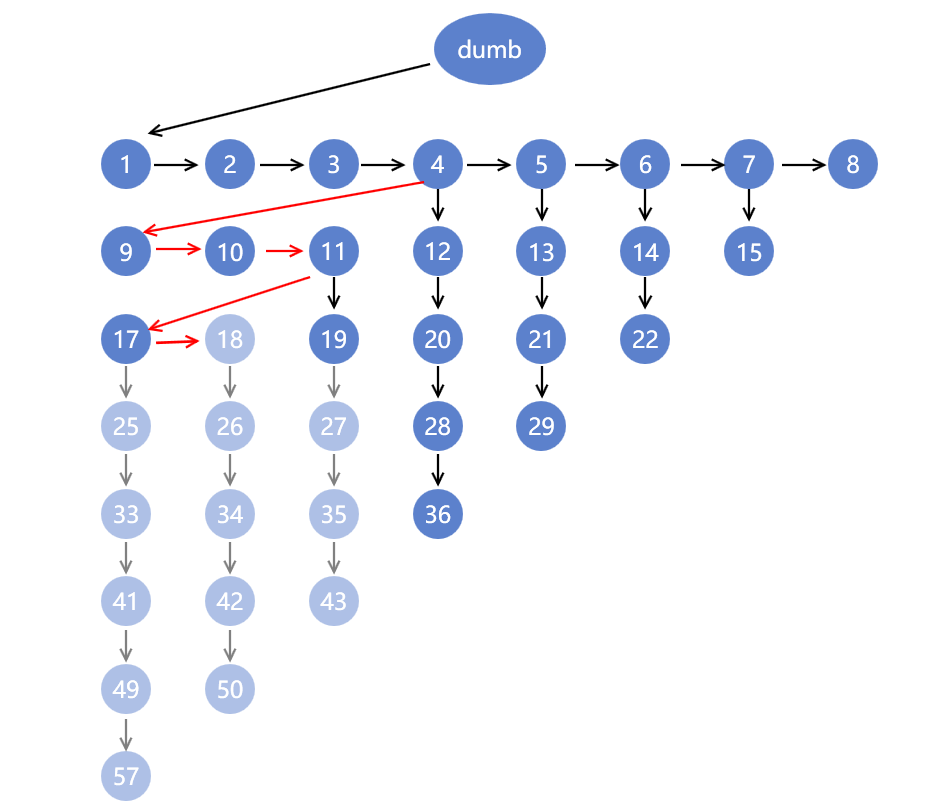
对节点 5,6,7,9,10,12,13,20进行比赛

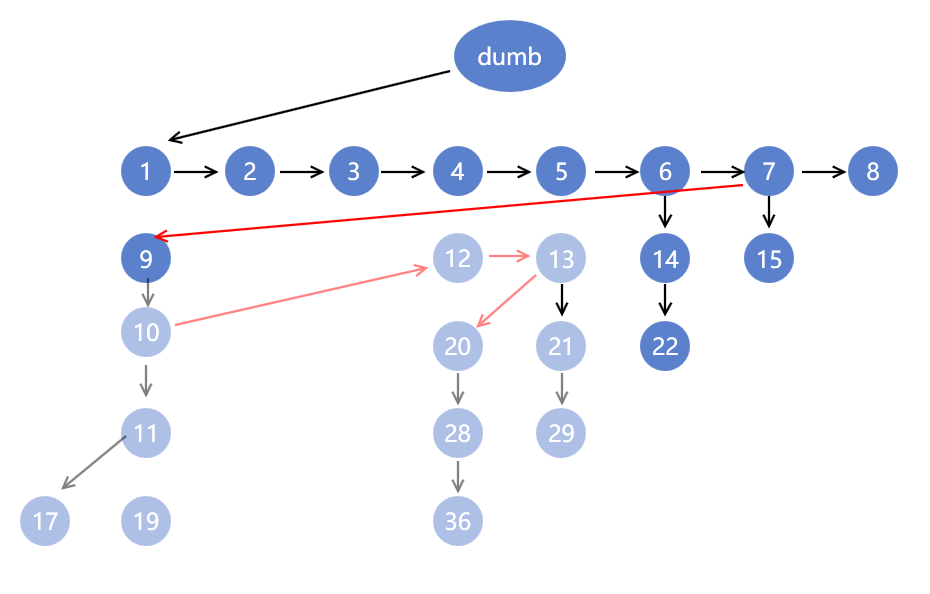
再对节点7，8，9，14，15，22进行比赛获得结果

所以总共为8+1+1+1=11次

最多次数

所以我们如果选择最多次数结果如下

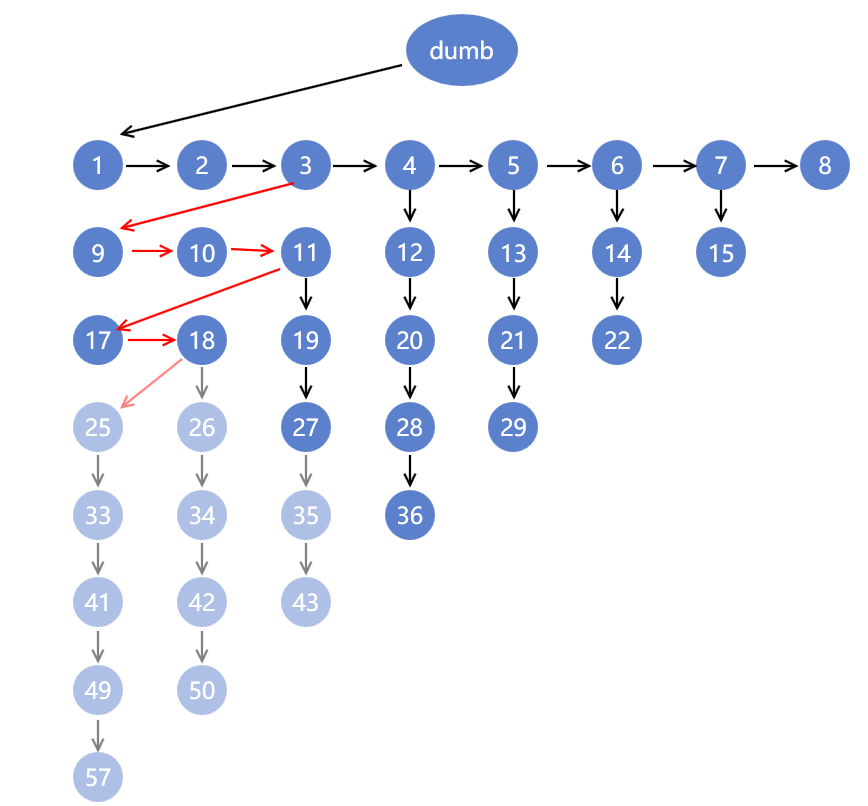
再选择节点4,9,5,10,12,11,20,13

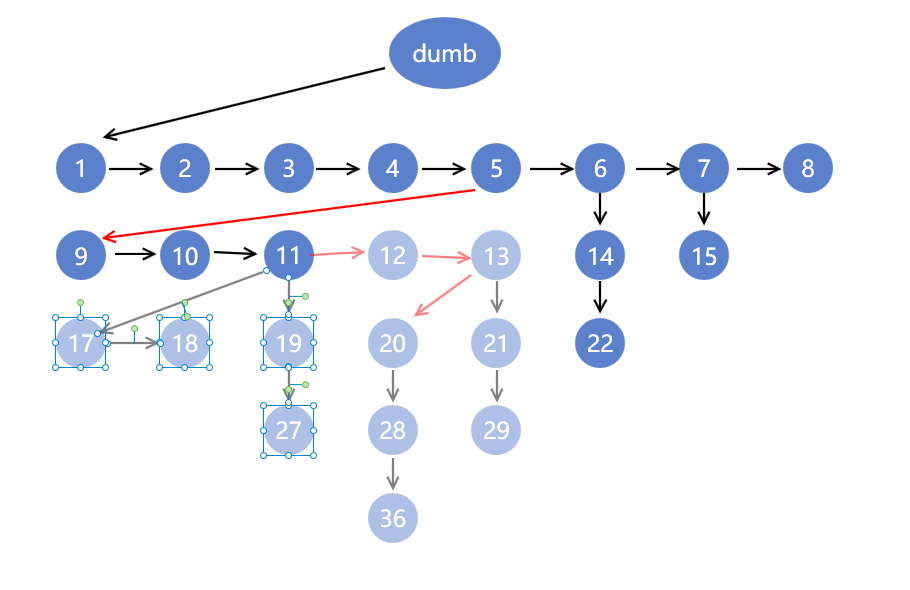
再选择节点6,7,9,10,11,14,15,22

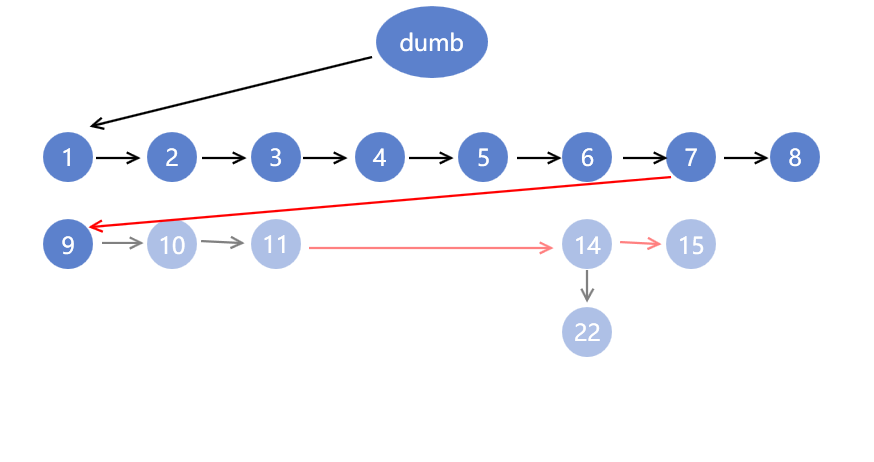
最后让节点8和9比一次

这样上限就是8+1+1+1+1=12次

算法实现

在算法实现上，可以定义一个树，

每次从最上层开始，选择同层节点数大于1的节点，进行比赛

然后更新树，使节点选择最深的层数，并且抛弃深度大于8的子树‘

直至树中每个节点有且仅有一个子节点。

扩展性想法

当然作为面试题，除了这样的过程，还可以有各种思路扩展：

• 比如如果可以计时，那么就可以8次跑完之类的

参考文档：